指從某個頂點作為起點,依照某種順序,一個一個拜訪所有能到達的頂點。
走訪的順序分為: 廣度優先 (Breadth First Search) 和 深度優先 (Depth First Search)。
假定某一頂點為起始起點(X),接著任意選擇一個與起點相鄰的頂點(Y),再接著選擇與頂點(Y)相鄰的頂點,一直任意選擇相鄰的頂點,直到找到某一個頂點的相鄰頂點都被走訪過,就回到上一個走訪的頂點,再繼續選擇相鄰的頂點,直到所有頂點都被走訪完。
取得任一頂點作為起始頂點(X),將其Push至堆疊Stack中。
若Stack不為空,則重複迴圈
-> 從Stack中Pop出一個頂點(Y)
-> 走訪頂點(Y),並將所有與頂點(Y)相鄰且尚未被走訪過且不存在於Stack的頂點,Push至Stack
迴圈結束
以下圖為例子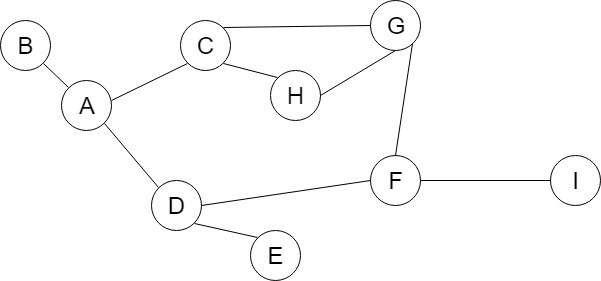
走訪頂點的時機: 將頂點從堆疊中POP出
其中一組拜訪順序為 A、D、F、I、G、H、E、C、B 的走訪步驟 :
| 步驟 | 說明 | 已走訪的頂點 | Stack (頂端)(尾) |
|---|---|---|---|
| (0) | 假設頂點A為起始點,Push(A) | 無頂點 | A |
| (1) | Pop(A),走訪頂點A。將與A相鄰且未走訪的點Push到堆疊中,Push(B,C,D) | A | B、C、D |
| (2) | Pop(D),走訪頂點D,將與D相鄰且未走訪的點Push到堆疊中,Push(E,F) | A、D | B、C、E、F |
| (3) | Pop(F),走訪頂點F。將與F相鄰且未走訪的點Push到堆疊中,Push(G,I) | A、D、F | B、C、E、G、I |
| (4) | Pop(I),走訪頂點I。與I相鄰的頂點F已被走訪過,故不進行Push | A、D、F、I | B、C、E、G |
| (5) | Pop(G),走訪頂點G。將與G相鄰且未走訪的點Push到堆疊中,Push(H) | A、D、F、I、G | B、C、E、H |
| (6) | Pop(H),走訪頂點H。與H相鄰的頂點G已被走訪過,而與H相鄰的頂點C已在堆疊中,故不進行Push | A、D、F、I、G、H | B、C、E |
| (7) | Pop(E),走訪頂點E。與E相鄰的頂點D已被走訪過,故不進行Push | A、D、F、I、G、H、E | B、C |
| (8) | Pop(C),走訪頂點C。與C相鄰的頂點A、H、G已被走訪過,故不進行Push | A、D、F、I、G、H、E、C | B |
| (9) | Pop(B),走訪頂點B。與B相鄰的頂點A已被走訪過,故不進行Push | A、D、F、I、G、H、E、C、B | 空 |
| (10) | Stack為空,迴圈結束 |
細談資料結構 第六版
ISBN 978-986-312-014-8

請問第二步為何不用push D節點?
嗨你好,是我遺漏了 D 節點 !
已經更新文章了呦 !
謝謝你認真閱讀 ~
![]()